Ошибки из-за флуктуации диаметра модового пятна

В методе оптической рефлектометрии распределение потерь в волокне находится по изменению рассеянной назад в волокне мощности зондирующих импульсов. Однако эта мощность изменяется не только из-за потерь в волокне, но и из-за вариаций коэффициента обратного релеевского рассеяния. По рефлектограмме, измеренной только с одной стороны волокна, нельзя определить, вызвано ли изменение рассеянной назад мощности потерями в волокне или изменением коэффициента обратного релеевского рассеяния. Поэтому вариации коэффициента обратного релеевского рассеяния приводят к появлению систематической ошибки при измерении потерь в волокне.

Наиболее сильно эта ошибка сказывается при измерении потерь в сростках волокон, где величина потерь обычно мала, а разность коэффициентов обратного релеевского рассеяния максимальна. При этом в месте соединения волокон часто наблюдается не только уменьшение сигнала из-за потерь, но и его увеличение (gainer). Поясним это явление на примере соединения двух волокон с постоянными по длине, но разными коэффициентами обратного релеевского рассеяния (рис. 3.19).

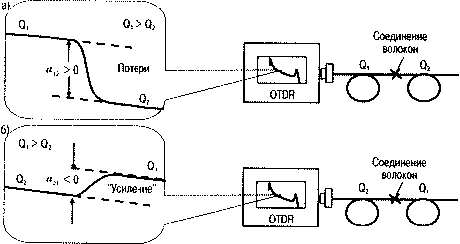
Рис. 3.19. Участок рефлектограммы вместе сварного соединения волокон с разными коэффициентами обратного релеевского рассеяния а) Рефлектометр подключен со стороны волокна с большим коэффициентом обратного релеевского рассеяния б) Рефлектометр подключен со стороны волокна с меньшим коэффициентом обратного релеевского рассеяния

Величина измеренных потерь в сростках волокон прямо пропорциональна десятичному логарифму отношения мощности обратной волны рассеянной в первом волокне (непосредственно до сростка волокон) к мощности обратной волны рассеянной во втором волокне (непосредственно за сростком волокон): . Когда рефлектометр подключен со стороны волокна с коэффициентом обратного релеевского рассеяния Q₁, то , где Тс - коэффициент пропускания сростка волокон. Если же рефлектометр подключен со стороны волокна с коэффициентом обратного релеевского рассеяния Q₂, то . Таким образом, выражения для потерь в сростках волокон измеренных во встречных направлениях (а₁₂ и а₂₁) можно записать в виде

а₁₂ = а_ист + Δа . . . . . . . . . . . . . . . . . . .
а₂₁ = а_ист + Δа . . . . . . . . . . . . . . . (3.9)

где a_ист = -10logТ_с - истинные потери в сростке волокон, а Δа = 5log(Q₁/Q₂) - систематическая ошибка, возникающая из-за разности коэффициентов обратного релеевского рассеяния.

При Q₁ > Q₂, систематическая ошибка Δа = 5log(Q₁/Q₂) > 0. Поэтому измеренное значение а₁₂ > а_ист > а₂₁. Т. е. при подключении рефлектометра со стороны волокна с большим коэффициентом обратного релеевского рассеяния величина измеренных потерь получается больше истинных потерь в сростке волокон, а при подключении рефлектометра с другой стороны меньше истинных потерь. Более того, если потери в сростке волокон настолько малы так, что выполняется условие а_ист < Δа, измеренное значение потерь а₂₁ может стать отрицательным. Т.е. будет наблюдаться кажущееся усиление сигнала, как это показано на рис. 3.19 б.

Оценим величину этой систематической ошибки. Для этого надо учесть, что коэффициент обратного релеевского рассеяния прямо пропорционален произведению коэффициента релеевского рассеяния αp на коэффициент захвата рассеянного излучения модой волокна S, а коэффициент захвата прямо пропорционален квадрату апертурного угла моды (θ) и обратно пропорционален квадрату диаметра модового пятна (w) (рис. 3.20).

Рис. 3.20. Доля мощности, рассеиваемая назад в моду волокна обратно пропорциональна квадрату диаметра модового пятна

В современных волокнах флуктуации коэффициента обратного релеевского рассеяния обусловлены, в основном, флуктуациями диаметра модового пятна. Учитывая, что величина коэффициента захвата обратно пропорциональна квадрату диаметра модового пятна, выражение для систематической ошибки можно записать в виде: Δа = 10log(w₂/w₁). В приближении Δw <<w, где w = (w₁ + w₂)/2 и Δw = w₁ - w₂, выражение для Δа приводится к виду: Δа = 4.34 Δw/w.

Разность диаметров модовых пятен (Δw = w₁ - w₂) является случайной величиной со средним значением (<Δw>) равным нулю. Поэтому для оценки a возьмем её среднеквадратичное значение: . При этом будем полагать, что диаметры модовых пятен распределены по нормальному закону с дисперсией равной σ². Тогда разность диаметров модовых пятен Δw также будет распределена по нормальному закону (с дисперсией 2σ²), а систематическая ошибка в этом случае будет равна: .

В спецификациях на волокна в качестве доверительного интервала принято указывать не σ, aΔw_д = 3σ, соответственно, величина систематической ошибки приближенно равна удвоенному отношению величины доверительного интервала к диаметру модового пятна:

. . . . . . . . . . . . . . . (3.10)

При типичных значениях w ≈ 10 мкм и Δw_д = 0.4 мкм получаем оценку: . Эта величина заметно больше средних потерь (~0.02 дБ) в сростках SM волокон и много меньше типичной величины полных потерь в линии (~20 дБ). Таким образом, при измерении полных потерь в линии систематической погрешностью можно пренебрегать и проводить измерения только с одной стороны линии. При измерении же потерь в сростках волокон систематическую погрешность, возникающую из-за разности диаметров модовых пятен, необходимо исключать.